Tutte's theorem

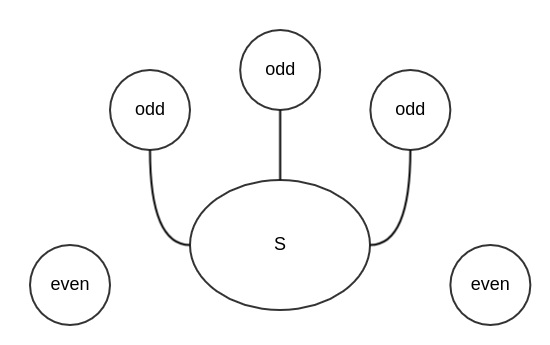
由 Tutte 於 1947 年提出，理論為 A graph G has a 1-factor iff o(G-S)<=|S| for every S ⊆ V(G)，而是理論也稱為該 graph G 的 Tutte's Condition

• o(G): 表示 graph G 的 odd components 的數量
• 1-factor: 等於 perfact matching 的狀態
• V(G): 表示 graph G 的 vertex 集合

並且可以知道其幾項性質：

• G 為一個 simple graph，vertex 數量記為 n (e.g. = n(G))
• o(G) ≡ n (mod 2), 指的是 o(G) 及 n(G) 同時為 even、或是同時為 odd
  • ≡: "定義"、"恆等於"
• For S ⊆ V:
  • o(G-S) ≡ n(G-S) = n - |S| (mod 2)
  • |S| + o(G-S) ≡ n(G) (mod 2) - 式(1)
• 而從 Tutte condition 可得第2式：
  • ∀S ⊂ V : o(G − S) ≤ |S|, - 式(2)
    • ∀: "任意存在"

證明與概念詳細解釋

從正向（Necessity）與反向（Sufficiency）證明

Necessity（必要性）

• 正面從 G 是為一個 1-factor 的圖做解釋，可以知道以這種情況下可以畫出圖形：

• 以性質來看
  • S 屬於 V(G)，而所有屬於 G-S 的 odd components 皆有一條 edge 連到 S 上
  • 而連到 S 內，則表示在 S 中必有同等數目的 vertices 與這條 edge 做對應的 endpoint，且互為 unique（不會重複使用 endpoint）
• 透過鴿籠原理，我們可以知道，以上圖為例，S 上有 3 個 odd components 與之連線，有 3 條 edges 進 S 當中，與之對應必有 3 個 unique 的 vertex，則 |S| >= o(G-S) 這條式子必成立

從正面去證明是直觀，並且簡單的；
而接下來是 tutte 的精華

Sufficiency（充份性）

• 這邊是從後面性質證回來，也就是說明擁有 o(G-S) <= |S| 性質的 graph，其必有 1-factor（perfact matching）的存在
  • == 假如 G 符合 Tutte's condition，則其有一 perfect matching (1-factor)
• 而我們可以使用反證法（擁有 o(G-S) <= |S| 性質，卻沒有 1-factor）來做證明，透過相同模型（分兩邊做討論），來分析各種情況，舉出擁有 1-factor 的實例，說明此假設錯誤，tutte's theorem 為真

先從假設的狀況下手

• 首先我們設定 S 為空集合，這樣從式(2)中可以得到 o(G-S) = o(G) ≤ |S| = 0，所以從式(1)當中可以知道 n(G) 是 even

    o(G-∅) = o(G) = 0, 表示沒有奇數 component!
    而此代表，graph G 的中 vertex 數量必定為 even !

Claim 1

增加一條 edge 並維持 Tutte Condition，也就是說，假設 e ∈ E(H)，而 H - e 符合 Tutte Condition（ 這個 H 就是加完 edge 並符合 Tutte Condition 的結果 ）

• 如何證明？

  • 我們可以先預設認為 H - e 符合 Tutte Condition
  • 而現在找一個 S，S ⊆ V (H)，屬於 H 的 vertex 集合
  • 當 e 的其中一個 endpoint 在 S 之中時，則 H - S = H - e - S ，這麼一來，便可以知道：

    o(H - S) = o(H - e - S) ≤ |S|

  • 否則，假設 J, J' 為 H - e - S 中的 Component，其內包含了 e 的 endpoint； 則可知其性質可分為以下幾種：

    

  • 而這幾種 case 都符合 o(H - S) ≤ o(H - e - S) ≤ |S|，則證明了 Claim 1 的假設符合 Tutte Condition

• 因此，假設 1-factor 的存在性並不足以使 graph 擁有 Tutte Condition 的話，則我們可以選擇一個 Maximal counterexample G，使這個 G 擁有幾項特性：
  • G 符合 Tutte Condition
  • 但 G 沒有 1-factor
  • 並且加入任何 single edge 進入 G 便可以產生一個 1-factor 的 graph （也就是目前的 G 是達飽和狀態前的 graph）

Claim 2

有了以上的認知後，我們可以接下來做；使用多個狀態來展示矛盾狀況即可證明。

• Idea:
  • 使用了 U 這個集合，並且我們把重點放在分析 G - U這個部份
  • U 的性質
    • 其內每個 vertex 的 degree 階為 n-1 (除了自己之外，對 graph G 內的每個 vertex 都有 edge 連通)

      U =  {v ∈ V | N(v) = V − {v} = {v ∈ V | dG(v) = n − 1}.
      N(v) 為 v 的 neighbor 集合，可以看到其集合為整個 Vertex Set，除自己以外的所有其他 vertex

• 有了以上的認知後，我們可以針對 G-U ，來先分為兩個情況下去做討論

Case 1

G-U 是為互不相連的 cliques（complete graph） 組成，如下圖所示：

• 而灰色的點則為 U，在圖中不畫出這些 U 內 vertex 的 edge
• 計算 o(G-U) = 4
  • 在圖中，有兩個 isolated vertices、一個 3-clique 以及一個 7-clique

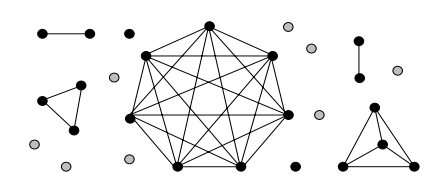
• |U| = 8

  • 透過 Tutte condition 以及 式(1)，U 擁有相同的性質： 大於等於 o(G-U)

• 接著可以建立 G-U 的 Maximum matching M (下圖中的紅色 edge)，試圖感染所有 G-U 的 components 中所有的 vertices

  • odd component 中的情況會是必有一個 vertex 無法被 matching 所感染
  • 而 even component 則是完美的感染完畢

• 接下來便是繼續加大這個 matching，以達到 graph G 的 perfect matching M'
  • 剛剛的步驟後，剩餘未被感染的 vertex 都在 odd components 當中
  • 所以我們可以透過讓這些 未被感染者，與 U 內的 vertex 建立 edge，來完成感染（下圖中綠色的部份）

• 到此為止，graph 當中沒有 matched 的 vertices 數量為 |U| - o(G-U)

  • 這些 vertices 都屬於 U，並且以 U 的性質來看，他們都是成對、並且相鄰的（其 degree 為所有 vertex 數量減 1）

  • 而這些 vertices 數量為偶數；

    
    為何為偶數？
    Ans: 因為可以從前面得知，目前 graph 的組成使用到了：
    (1) 偶數的 components -> 提供 even number 的 vertices
    (2) 奇數的 components -> 提供 odd number 的 vertices
    (3) 而 U 內與奇數 components 相連使用的 vertices -> odd
    而在一開始假設那段，我們可以知道再情況下， graph 的 vertice 總數量為 even ！
    那麼從上面可知，even（總數）- even（偶數 comp.）- odd（奇數 comp.） - odd（U 內對應的 vertices）後的結果，必為偶數！(U 內剩餘的 vertices)

  • 由於剩餘的互相為 pairwise adjacent vertices，這些 vertice 可以自行形成 perfect matching (下圖中藍色部份)

這麼一來，Case 1 的狀態便分析完畢

Case 2

G-U 並非互不相連的 cliques（complete graph）的情形。如下圖：

• 設 H 為其中一個 G-U 中的 component，並且不為 clique.

  • 其至少有 3 個 vertices，其中兩個之間的距離必為 2（因為其不為 clique 的緣故）；比如上圖中 H 內的 x, z
  • 而 x, z 中有一個相同的鄰居 y
  • 並且存在一個 w，其屬於 G-U 的 vertex set 當中，並且 wy 之間的 edge 並不存在

    注意：
    w 可能不一定屬於 H

  • 相同地，灰色的 vertices 表示 U 集合，每個 vertex 的 edge 都忽略不畫上去（影響重點）

• 回到 G 的部份，當加入一個 single edge 進 G 後，則會產生一個 perfect matching； 根據此，我們假設了兩個 matching - M1(藍色) = G + xz 以及 M2(紅色) = G + wy，如下圖所示：

• 當中，虛線的 xz, wy 並不屬於 G
• 設 F = M1 及 M2 的 symmetric difference；而 xz,wy 則屬於 F
  • 透過先前的 Lemma 所知， F 內的 component 為一條 path 或是 even cycle
  • 而實際上，當 F 內 component 是為 path 時，表示這些都是 isolated 的 vertex；否則其 endpoints 就不會被 M1 或是 M2 所感染
• 以上圖看，則 component C 是為包含 xz 的 even cycle

而針對這個 component C 再下去做分析，則可以再分為兩個 case 做討論：

Case 2A

yw 不屬於 C 時，則 M1 與 C 取 symmetric difference 的結果等於 M2 與 E（C）取交集 再與 M1 扣除 E（C）後的結果做聯集，其結果為一 perfect matching 且不包含 xz 或是 wy，合法屬於 G 的 perfect matching

Case 2B

yw 屬於 C，則我們可以稍微改一下上面圖，並標示出每個屬於 C 的 vertex: w,y,a1,a2,...,ap,z,x,b1,b2,...,bq

• 其中上面的 p, q 皆為 odd

  • 因為 path y,a1,...ap,z 這段上面， M1 及 M2 必須有相同數目的 edges
  • 因此 edge 數目為 even，vertex 數量則為 odd
  • 又 |V(C)| = 4 + p + q， 為 even !
  • 所以 p, q 相同都為 odd

• 所以 edge 集合為 M*

  • M* = {a1a2, ... , a(p-2)a(p-1), a(p)z, yx, b1b2, ... b(q-2)b(q-1), bqw} ，都屬於 E 集合（edge 總集合）
  • 於下圖中綠色部份展示為一組 perfect matching 於 V(C)
  • 下圖中黃色部份是展示 M1 - E(C) 為一組 perfect matching 於 V - V(C)
  • 而這兩組取聯集後，成為 G 的一組 perfect matching ！ 因此符合 Tutte Condition !

如此我們便可以說，在符合 tutte condition 情況下，其必定有 1-factor 的存在

Summary

Case 1 的部份較為簡單，透過鴿籠原理即可證實。

Case 2 的部份主要是以一直符合 Tutte Condition 的 graph G，在差一條 edge 可以成為 "1-factor" G' 的假設為前提下去做的分析，透過證實在差一條 edge 可成為 1-factor 的這個性質來強調，分析下的 graph 皆為假設下沒有 1-factor 的這個情形。所以從這個 G 下去做分析，來證實 只要符合 tutte condition，就一定有 1-factor 存在 這個性質，說明前面假設部份為錯誤的假設情況。

Reference

• notes-March15.pdf